LAS FIGURAS GEOMÉTRICAS SON:
Una figura geométrica es un conjunto no vacío cuyos elementos son puntos. Las figuras geométricas son el objeto de estudio de la geometría, rama de las matemáticas que se dedica a analizar las propiedades y medidas de las figuras en el espacio o en el plano.
PERÍMETRO: es la suma
de los lados de una figura geométrica. Es su contorno.
EJEMPLO:
Los lados del rectángulo de la figura miden 10 cm. y 5 cm.
10 cm
|
 |
10 cm
|
El perímetro del rectángulo lo obtenemos sumando todos sus lados:
Perímetro = 10 cm + 5 cm + 10 cm + 5
cm = 30 cm
|
Por lo tanto, el perímetro
del rectángulo es 30 cm.
ÁREA: es la medida de la superficie de una figura; es decir, la medida
de su región interior.
ÁREA DE UN
 |
El área del rectángulo corresponde a la medida de la región verde, y se
obtiene multiplicando
la base por la altura.
la base por la altura.
Área = base · altura
|
EJEMPLO:
Los lados del rectángulo de la figura miden 10 cm. y 5 cm.
10 cm
|
La altura de este rectángulo mide 5 cm.
|
 |
|
10 cm
|
La base de este rectángulo mide 10 cm.
|
Área = 10 · 5 = 50 cm2
|
el área del rectángulo es 50 cm2
TRIANGULO.
Triángulo es la figura plana formada por una poligonal
cerrada de tres lados, o bien, la figura formada por tres rectas que se cortan,
a los puntos de corte se les llama vértices.
CUADRADO.
Un cuadrado es una figura geométrica que tiene cuatro lados iguales
unidos por los extremos, y que posee dos diagonales, también iguales, que se unen
en el centro exacto.
Su área y su perímetro son:
Rectángulo.
Un rectángulo
es un polígono de 4 lados (una figura plana de lados rectos) en donde cada
ángulo es un ángulo recto (90°).
Su perímetro y área son:
Una figura de cuatro lados que tiene todos sus lados de una misma
longitud.
Su área y
perímetro son:


Trapecio.
El Trapecio es un cuadrilátero con un par de lados paralelos, pero de
distinta longitud que se denominan bases. Sus otros dos lados no son paralelos.
Área y perímetro de un trapecio:
P =a+b +c+d
Paralelogramo.
Un paralelogramo es un tipo especial de cuadrilátero (un polígono formado
por cuatro lados) cuyos lados opuestos son iguales y paralelos dos a
dos.
Área y perímetro de un paralelogramo:
P = 2· b + 2· c = A=
b · a = 2 (b + c)
Área y perímetro de los polígonos regulares.
En geometría, se le llama polígono regular a un
polígono cuyos lados y ángulos interiores son congruentes entre sí. Los
polígonos regulares de tres y cuatro lados se llaman triángulo equilátero y
cuadrado, respectivamente. Para polígonos de más lados, se añade el término
regular (pentágono regular, hexágono regular, etc).
El Perímetro es la longitud de
un lado por el número de lados. P = N · L
¿ qué son los Cuerpos geométricos?
Llamamos cuerpos geométricos a
los sólidos que
ocupan un lugar en el espacio. Es decir que los podemos tocar, medir y pesar.
Las medidas se toman en longitud, anchura y altura.
Los cuerpos geométricos se dividen en dos grupos: poliedros y los cuerpos redondos.
VOLÚMENES DE LOS CUERPOS
GEOMÉTRICOS.
Para calcular un volumen necesitamos tres dimensiones: largo, ancho y alto. El producto de los valores largo X ancho X alto nos da el volumen.
Es lo mismo que decir, el volumen lo calculamos también multiplicando el área de la base por la altura.
Poliedros regulares.
Los poliedros regulares tiene todos sus ángulos diedros y todos sus
ángulos poliedros iguales y sus caras son polígonos regulares iguales.
- Volumen del Tetraedro:
Es un poliedro de cuatro caras.
- volumen del cubo.
Un cubo o hexaedro regular es un poliedro de seis caras cuadradas congruentes, siendo uno de los llamados sólidos platónico.
- Volumen del octaedro.
Es un poliedro de ocho
caras.
- Volumen del prisma.
un prisma es un poliedro con
una base poligonal de n lados, una copia de traslación (no en el mismo plano que la primera), y otras n
caras (todas necesariamente deben ser paralelogramos)
que une los lados correspondientes de las dos bases.
- Volumen del Ortoedro.
Un ortoedro o cuboide es un paralelepípedo ortogonal, es decir, cuyas
caras forman entre sí ángulos diedros rectos. Los ortoedros son prismas
rectangulares rectos, y también son llamados paralelepípedos rectangulares.
- Volumen de la pirámide.
Una pirámide es un poliedro limitado por una base, que es un polígono
con una cara; y por caras, que son triángulos coincidentes en un punto
denominado ápice.
El ápice o cúspide también es llamado vértice de la pirámide, aunque una
pirámide tiene más vértices, tantos como el número de polígonos que lo limitan.
- Volumen del tronco de pirámide.
El tronco de pirámide es un poliedro comprendido entre la base de la
pirámide y un plano que corta a todas las aristas laterales.
- Volumen del cilindro.
un cilindro es una superficie de las denominadas cuadráticas formada por
el desplazamiento paralelo de una recta llamada generatriz a lo largo de una
curva plana, que puede ser cerrada o abierta, denominada directriz del cilindro.
- Volumen del cono.
un cono
recto es un sólido de revolución generado por el giro de un triángulo
rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro
cateto se denomina base y al punto donde confluyen las generatrices se llama vértice.
- Volumen del tronco de cono.
El tronco de cono, cono truncado o tronco de Garófalo es un volumen de
revolución generado por un trapecio rectángulo al tomar como eje de giro el
lado perpendicular a las bases.
- Volumen de esfera.
una superficie esférica es una superficie de revolución formada por el conjunto de los puntos del espacio cuyos puntos equidistan de otro interior llamado centro. Los puntos cuya distancia es menor que la longitud del radio forman el interior de la superficie esférica. La unión del interior y la superficie esférica se llama bola cerrada.
- Volumen de la semiesfera.
Una semiesfera es cada una de las partes de una esfera comprendida entre
dos planos que se cortan en el diámetro de aquella.
- Volumen de la cuña esférica.
La cuña esférica es la parte de una esfera comprendida entre dos planos
que se cortan en el diámetro de aquella.
- Volumen del casquete esférico.
Un casquete esférico, en geometría, es la parte de una esfera cortada por un plano. Si dicho plano pasa por el centro de la esfera, lógicamente, la altura del casquete es igual al radio de la esfera, y el casquete esférico será un hemisferio(semiesfera).
- Volumen de zona esférica.
En geometría, se denomina segmento esférico al sólido definido por
cortar una esfera con un par de planos paralelos.







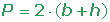










.jpg)













.jpg)




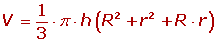


.jpg)

.jpg)



.jpg)

2 comentarios :
Me parece que su blog es muy interesante y creativo.
...
Publicar un comentario